LeetCode 筆記 - 5. Longest Palindromic Substring

Posted on

題目在此 5. Longest Palindromic Substring

給定一個字串，找出最長迴文子字串

解題思維

這題無論用暴力硬掃或者 dynamic programming 都可以
不過複雜度都是 O(n²)
(根據 Longest Palindromic Subsequence | DP-12)

這題推薦使用 Manacher’s Algorithm
可以利用迴文的特性，將複雜度降到 O(n)

Time complexity: O(n)

Manacher’s Algorithm

這個神奇的演算法是一位叫 Manacher 的人在 1975 年發明的 (太神啦！
為什麼每篇教學文都要講到 1975 年

接下來讓我們一步步的把 Manacher’s Algorithm 建立起來

前置動作

首先這個演算法需要對字串做一些前處理
這主要是為了可以讓 奇數 與 偶數 長度的迴文判斷都變成同一個邏輯 (奇數)

1
padding_string = f"^_{'_'.join(string)}_$"

例如

1
2
3
4
5
6
7
8
s0 = "lloll"
s1 = "llooll"

padding0 = "^_l_l_o_l_l_$"
padding1 = "^_l_l_o_o_l_l_$"

result0 = '_l_l_o_l_l_' # 11
result1 = '_l_l_o_o_l_l_' # 13

計算迴文半徑

接下來我們需要一個 list 來存放資料
每一個 index 存放的資料是 以 index 為中心，可以找到最大的迴文字串半徑

舉例

1
2
3
4
s0 = "lloll"

padding0 =    "^_l_l_o_l_l_$"
# PLS_radius = 0012105012100

看，是不是很神奇

中心擴展算法

在這裡就是很直觀的判斷上下界
接著前後 (中心 - 半徑) 與 (中心 + 半徑) 兩個字元比對
最終得到結果

1
2
3
4
5
6
7
8
9
10
11
PLS_radius = [0] * padding_length

for center_index in range(padding_length):
    LPS_result = 0
    for i in range(LPS_result, padding_length):
        if center_index - i < 0 or center_index + i >= padding_length:
            break
        if padding_string[center_index - i] != padding_string[center_index + i]:
            break
        LPS_result = i
    PLS_radius[center_index] = LPS_result

其實到這裡，就已經可以找到我們要的答案
但如果就只是單純的使用中心擴展算法
就只是個 O(n²) 的演算法而已

接下來 Manacher’s Algorithm 的威力才正要開始

利用迴文特性加速

在這裡我們需要先了解一個概念

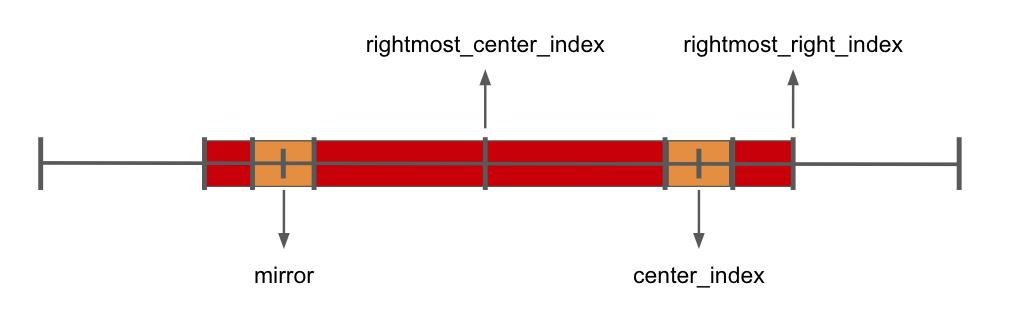
image 18

那就是在一個迴文字串裡，如果出現一個子迴文，那另一邊也會出現 一樣長度 的子迴文
見圖中橘色區塊

center_index 是目前正在檢查的 index
這時候我們會利用涵蓋最多右邊資訊的最右邊的迴文字串中心來計算出 mirror
查看 mirror 的位置最長迴文字串長度

進而得知 PLS_radius[center_index] 至少會多少起跳

好，這時候可能會有三種情況

第一種
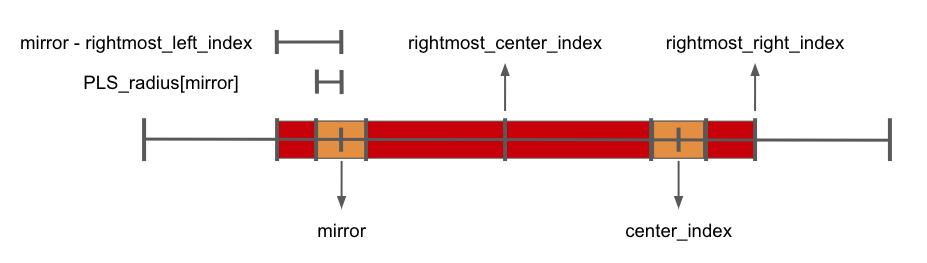
image 19

就是橘色部分沒有超過靠右邊的迴文字串的範圍
這個判斷我們可以透過比對 mirror - rightmost_left_index 與 PLS_radius[mirror] 得知

也就是說 mirror - rightmost_left_index > PLS_radius[mirror]

所以 PLS_radius[center_index] = PLS_radius[mirror]

第二種
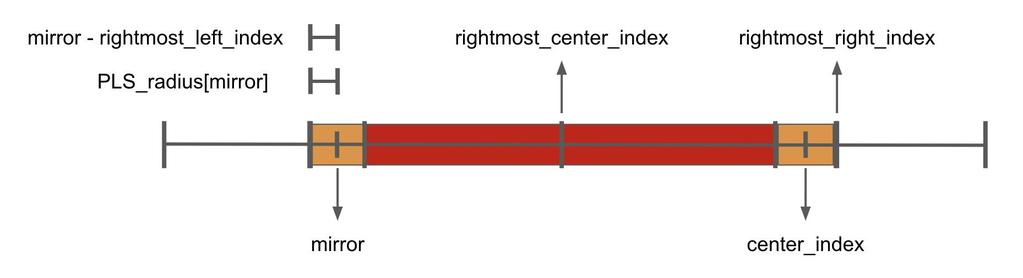
image 20

橘色部部分邊界剛好等於靠右邊的迴文字串的範圍
也就是說 mirror - rightmost_left_index = PLS_radius[mirror]

所以 PLS_radius[center_index] = PLS_radius[mirror]

第三種
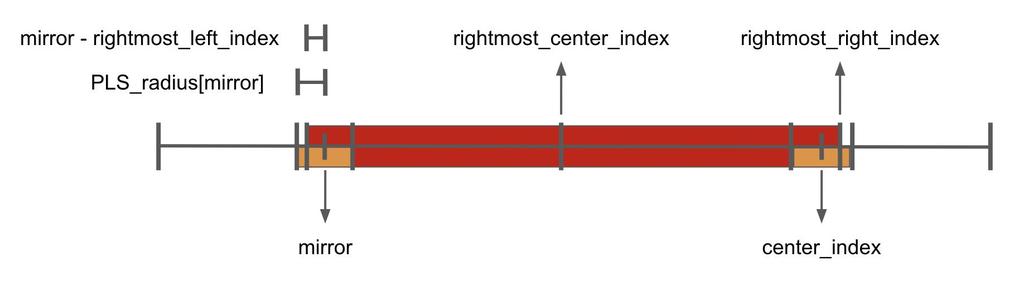
image 21

橘色部部分邊界超過靠右邊的迴文字串的範圍
也就是說 mirror - rightmost_left_index < PLS_radius[mirror]

我們可以在圖中看到右邊的橘色超出了一點
但對右邊的橘色迴文字串來說，那超出的一點是未知的狀態

所以 PLS_radius[center_index] = mirror - rightmost_left_index

比對完畢

接下來中心擴展算法，就可以直接從剛剛三種方法判斷來的長度再接下去比對了
如此一來你會發現中心擴展算法因為使用了過去的長度與迴文的特性

進而實現了 O(n) 的時間複雜度

太神啦！

程式碼

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
class Solution:

    def longestPalindrome(self, s: str) -> str:

        if len(s) < 2 or s == s[::-1]:
            return s
        
        # 前處理
        padding_string = f"^_{'_'.join(s)}_$"
        padding_length = len(padding_string)
        
        # 紀錄了以 index 為中心，可以拓展的迴文字串半徑
        PLS_radius = [0] * padding_length

        rightmost_right_index = 0
        rightmost_center_index = 0
        for center_index in range(padding_length):

            LPS_result = 0

            if center_index < rightmost_right_index:
                # center_index - (center_index - rightmost_center_index) * 2
                # center_index - center_index * 2 + rightmost_center_index * 2
                # rightmost_center_index * 2 - center_index

                mirror = 2 * rightmost_center_index - center_index

                # at first, remember
                # rightmost_right_index - center_index = mirror - rightmost_left_index

                # case 0: PLS_radius[mirror] < rightmost_right_index - center_index
                # 表示以 mirror 為中心的迴文字串沒有超過，目前最靠右邊的迴文字串範圍
                # 因為會以 rightmost_center_index 對稱，所以 PLS_radius[center_index] 會等於 PLS_radius[mirror]

                # case 1: PLS_radius[mirror] == rightmost_right_index - center_index
                # 表示以 mirror 為中心的迴文字串剛好等於目前最靠右邊的迴文字串範圍
                # 那就以 rightmost_right_index 開始掃描就可以了
                # PS: center_index + rightmost_right_index - center_index = rightmost_right_index

                # case 2: PLS_radius[mirror] > rightmost_right_index - center_index
                # 表示以 mirror 為中心的迴文字串超過，目前最靠右邊的迴文字串範圍
                # 因為超過 rightmost_right_index 的地方是未知
                # 所以從 rightmost_right_index 開始掃描
                # PS: center_index + rightmost_right_index - center_index = rightmost_right_index

                LPS_result = min(rightmost_right_index - center_index, PLS_radius[mirror])

            # 中心擴展算法
            for i in range(LPS_result, padding_length):
                if center_index - i < 0 or center_index + i >= padding_length:
                    break
                if padding_string[center_index - i] != padding_string[center_index + i]:
                    break
                LPS_result = i
            PLS_radius[center_index] = LPS_result

            if center_index + LPS_result > rightmost_right_index:
                # 更新最右迴文字串右邊界
                rightmost_right_index = center_index + LPS_result
                # 更新最右迴文字串中心點
                rightmost_center_index = center_index

        max_center_index = max_length = 0
        for i, p in enumerate(PLS_radius):
            if p > max_length:
                max_length = p
                max_center_index = i

        result = s[(max_center_index - max_length) // 2:(max_center_index + max_length) // 2]

        return result

擴展中心演算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution:
    def longestPalindrome(self, s: str) -> str:
        if len(s) <= 1:
            return s

        def expand_from_center(left, right):
            while left >= 0 and right < len(s) and s[left] == s[right]:
                left -= 1
                right += 1
            return s[left + 1:right]

        max_str = s[0]

        for i in range(len(s) - 1):
            odd = expand_from_center(i, i)
            even = expand_from_center(i, i + 1)

            if len(odd) > len(max_str):
                max_str = odd
            if len(even) > len(max_str):
                max_str = even

        return max_str

也許你也會想看看