題目在此 329. Longest Increasing Path in a Matrix
![image 24]()
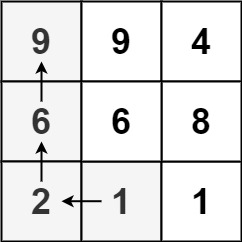
給一個 matrix,請計算出最長遞增路徑的長度
解題思維
這題的基本思維是做 n x m 次的 Depth First Search
但其實在每一次的 Depth First Search 之間,我們是可以利用之前計算的結果來加速的
宣告一張表,裡面存放的資訊是,該點可以找到的最長遞增路徑
而 Depth First Search 的過程中當某一個點遇到附近已經有結果的點
那就不用對有結果的點遞迴下去,因為已經跑過了,直接把結果拿過來用就可以了
完成 ✅
程式碼
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
| class Solution:
def longestIncreasingPath(self, matrix: List[List[int]]) -> int:
def get_neighbors(y, x):
offset = [-1, 1]
result = []
for o in offset:
new_y = y + o
if not 0 <= new_y < length_y:
continue
if matrix[new_y][x] <= matrix[y][x]:
continue
result.append((new_y, x))
for o in offset:
new_x = x + o
if not 0 <= new_x < length_x:
continue
if matrix[y][new_x] <= matrix[y][x]:
continue
result.append((y, new_x))
return result
length_y = len(matrix)
length_x = len(matrix[0])
long_map = [[0 for _ in range(length_x)] for _ in range(length_y)]
def dfs(y, x):
if long_map[y][x] != 0:
return long_map[y][x]
neighbors = get_neighbors(y, x)
if not neighbors:
long_map[y][x] = 1
return 1
max_path_legnth = 0
for n_y, n_x in neighbors:
max_path_legnth = max(dfs(n_y, n_x), max_path_legnth)
long_map[y][x] = max_path_legnth + 1
return max_path_legnth + 1
result = 0
for y in range(length_y):
for x in range(length_x):
if long_map[y][x] != 0:
continue
result = max(result, dfs(y, x))
return result
|
也許你也會想看看