追尋多年的三角棋
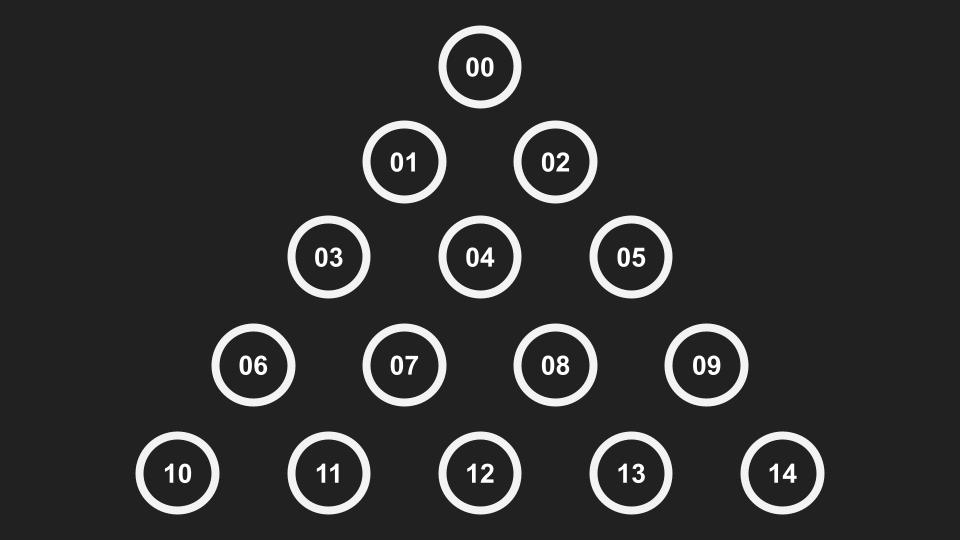
三角棋或三角殺棋[1],開始時共有 15 個圈圈,每個回合玩家可以畫一個直線,消掉相鄰的一到三顆
輪流畫到最後一顆的人輸
這篇文
代表了長達至少六年的追尋,而現在的我終於可以為這件事畫下句點了
三角棋,是我從國小就常常玩的遊戲,一直玩到高中畢業
雖然整理出一些規則之後就沒有輸過,但我清楚知道心裡一直有一個疑問沒有被滿足
這真的是最終解答了嗎?
在這之前,我想先描述一下這一切的開始
殘局理論
因為規則是畫到最後一顆輸,那如果往前看前幾個步驟,就會發現把一些特定形狀留給對手是一定會贏的
最常見的就是
2 2
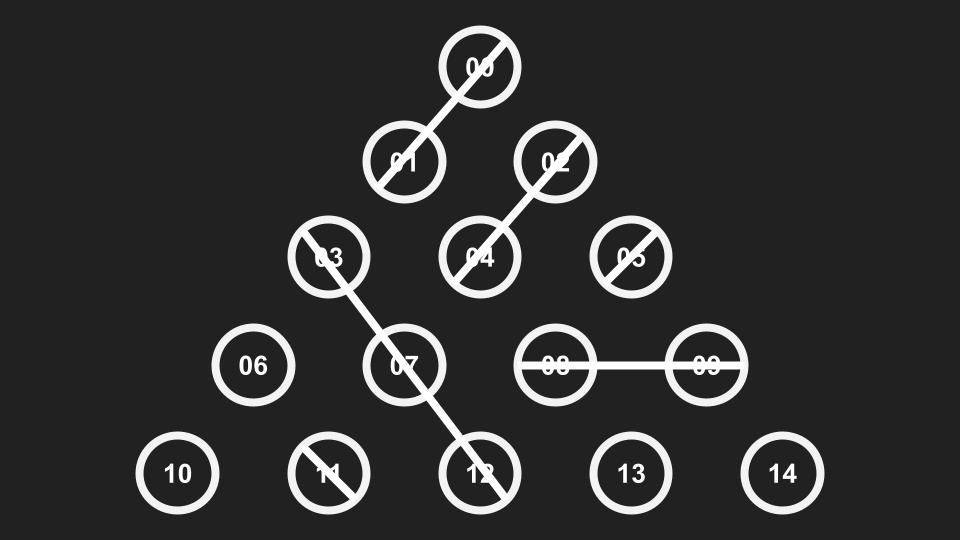
3 1
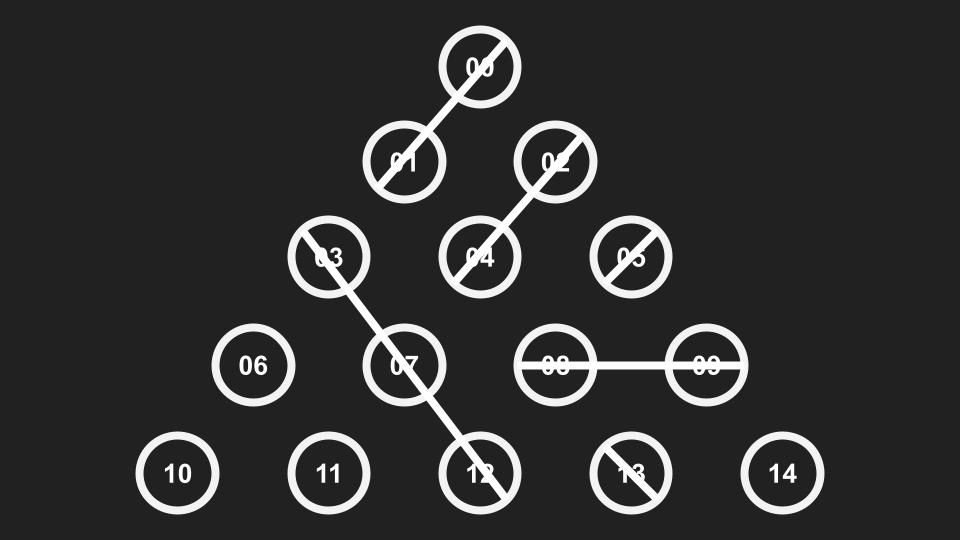
1 2 3
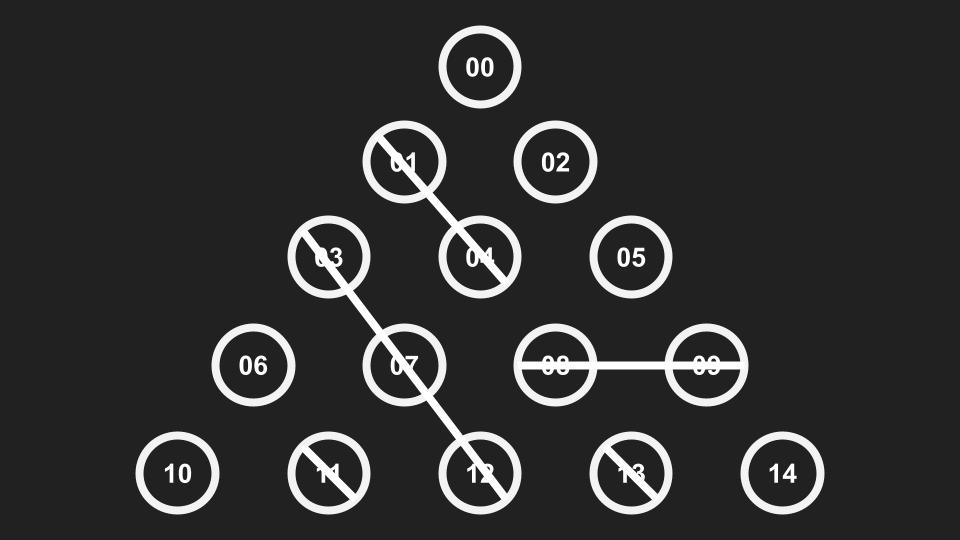
等等的…大概十種殘局可以背
其實用到殘局理論就等於比對手多思考幾步,實戰下來勝率已經很高了
但這遠遠還不夠
先手必勝理論
這個理論是假定有某個開局存在必勝路徑,但是還不會寫程式驗證的我
只能花時間去追尋不知道存不存在的必勝開局
下面這個開局,我贏了高中兩年多的時間,概念上是盡可能畫多一點,盡快進入殘局
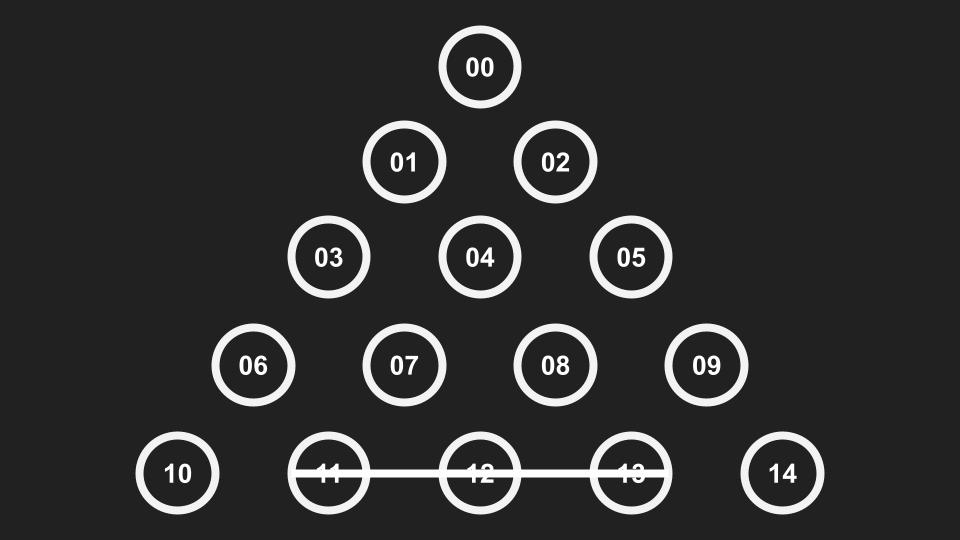
根據程式分析這個開局勝率有 95 %
直到我的高中兼大學同學狗勾,找到完美應對
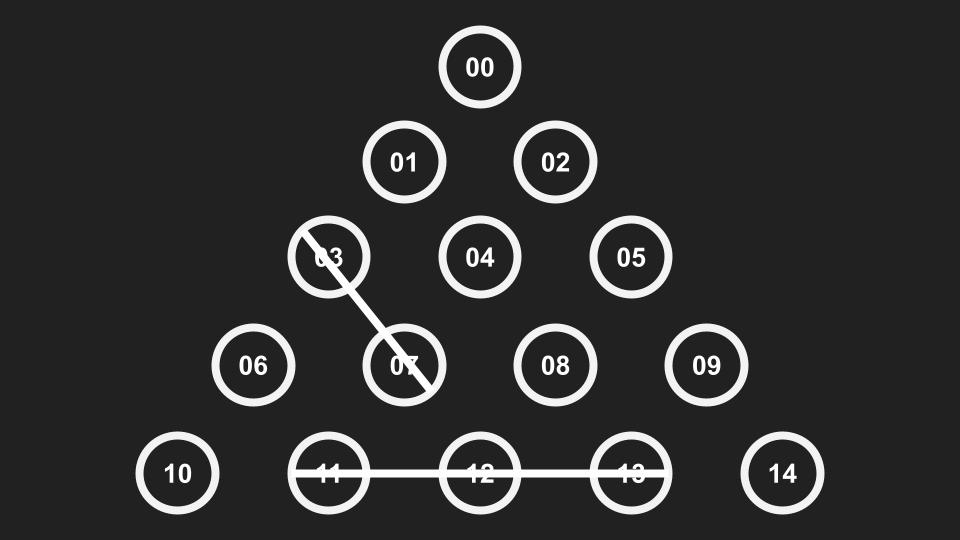
這個應對後來也被程式驗證為 100 % 勝率,無解
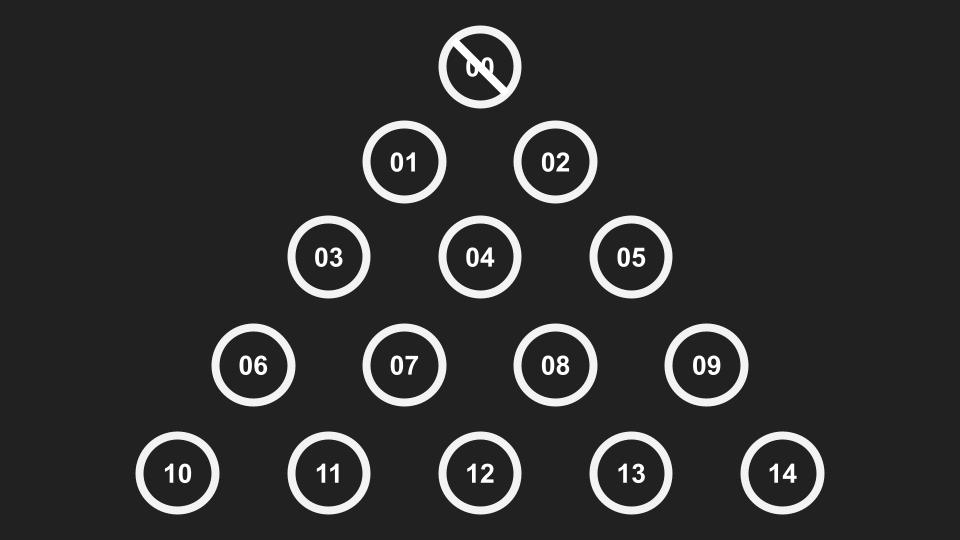
後來下面的開局,開啟了無敗紀錄
概念是使用最小化的開局,根據對方的應對,在我的第二手就決定勝負!
透過之前的殘局理論讓對手沒辦法留下會讓我輸的殘局給我
不過,每贏一局
那個疑問都會再一次浮在我的心裡
這是我追尋的終點嗎?
當時我知道我還沒有辦法解開這個謎團
這個問題只能放在心裡,留待未來的我來解答
程式解答
直到 2018 年的某一天,我回想起三角棋並順利地把程式寫出來
沒想到
除了驗證無敗紀錄用的開局,是真的存在必勝路徑
還額外找到兩種開局都存在必勝路徑
終於,走到了終點
以下是存在必勝路徑的九種開局(包括旋轉的情況)
- 0
- 3
- 4
- 5
- 7
- 8
- 10
- 12
- 14
大家可以到專案位置,實際玩玩看也可以跑跑看所有開局的獲勝機率
https://github.com/PttCodingMan/TriangularNim
僅以此文獻給陪我玩三年的高中兼大學同學狗勾